算法学习笔记(二)
前言
最近发现,笔记的引言部分都变成了我笔记里的槽点,所以在下干脆把这个引言改成前言,以后就用来记录一些我写这篇笔记的心情和想法,以便我日后回过头来看哈
求从始点到终点的最短路径
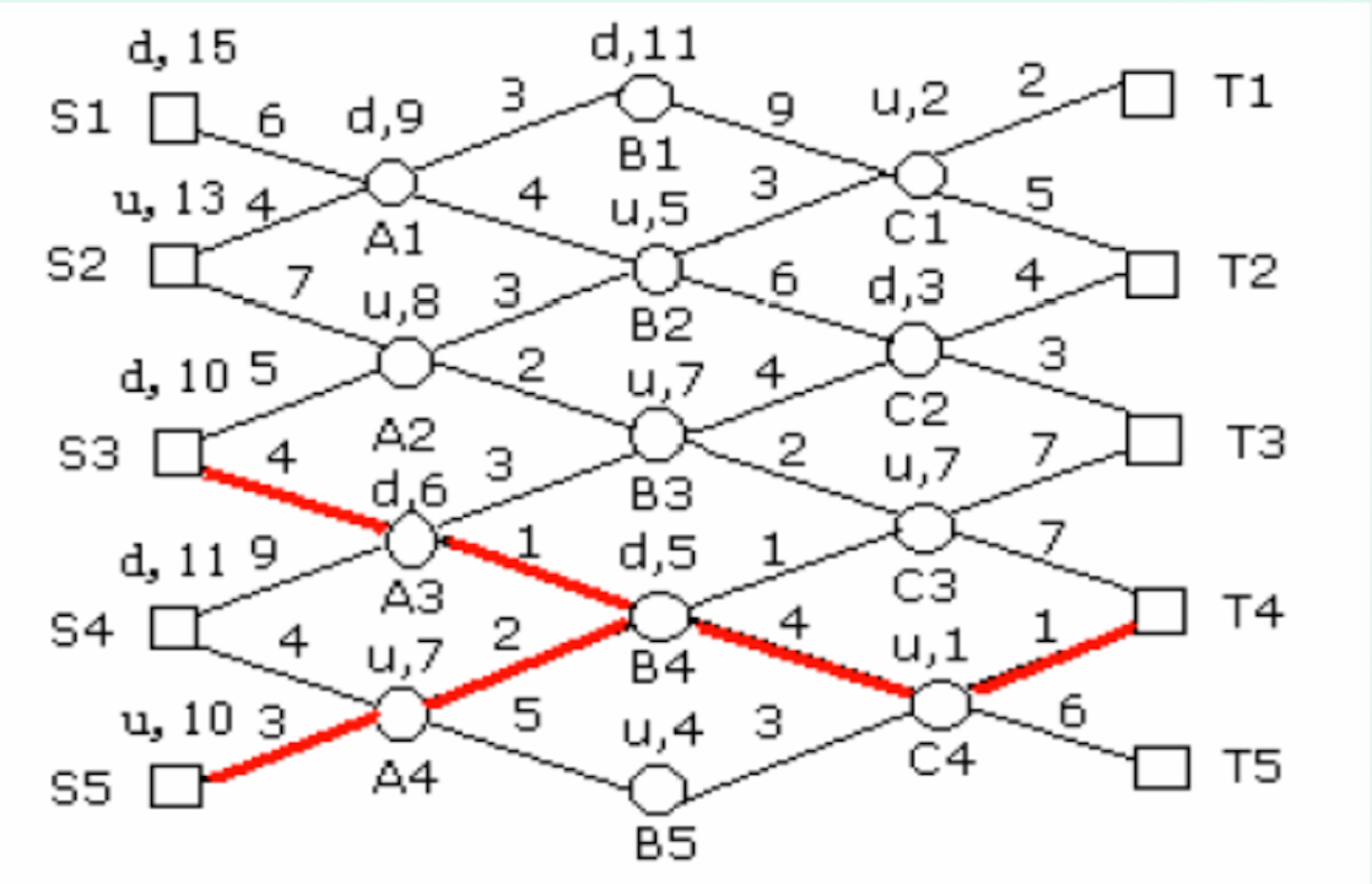
实现思路
任何最短路径的子路径都是相对于子路径的始点和终点的最短路径
为找到一条最短路径只需从Tj开始进行多步判读
判断序列:
- F(Cl) = min{ C1->Tm }
- F(Bk) = min{ BkCl + F(Cl) }
- F(Aj) = min{ AjBk + F(Bk) }
- F(Si) = min{ SiAj + F(Aj) }
代码实现
// todo
计算二项式系数
实现思路
二项式系数,记作C(n,k)或者 ,是来自于一个n元素集合的k元素组合(子集)的数量(0≤k≤n)
规律:
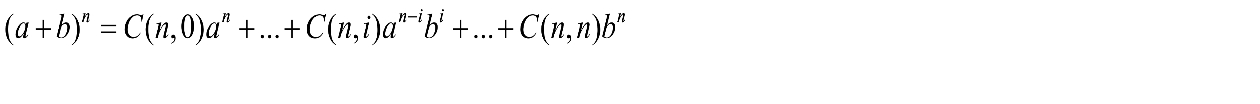
递推性:
C(n, k) = C(n-1, k-1) + C(n-1, k), 当n > k >0 C(n, 0) = C(n, n) = 1
代码实现
@RequiresApi(api = Build.VERSION_CODES.N)
public int binomial(int n, int k) {
int[][] C = new int[n + 1][k + 1];
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= Integer.min(i, k); j++) {
if (j == 0 || j == i) {
C[i][j] = 1;
} else {
C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
}
}
}
return C[n][k];
}
01背包问题
实现思路
Sk = {前k个物品装入背包的最优方案}
递归公式:
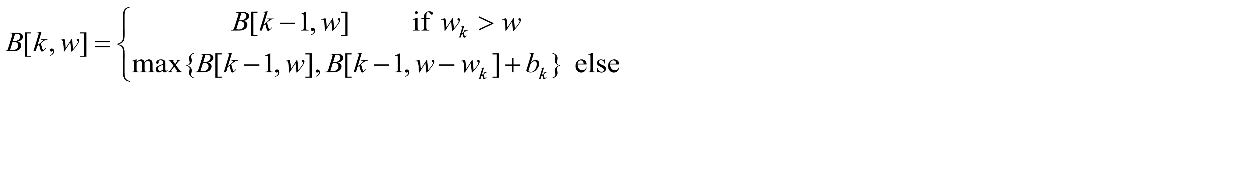
在空包状态下,前k个物品Sk在容量为w时的最优解由如下两部分构成:
- 第k个物品放不进去背包前k-1个物品Sk-1在容量为w时的最优解
- 第k个物品放得进去背包 (放入 或 不放入)前k-1个物品Sk-1在容量为w-wk 的最大收益 + 第k个物品的收益
代码实现
public int bagOf01Solve(List<Item> items, int limitWeight) {
int N = items.size();
int W = limitWeight;
int[][] B = new int[N + 1][W + 1];
for (int i = 1; i <= N; i++) {
for (int w = 0; w <= W; w++) {
if (i == 0 || w == 0) {
B[i][w] = 0;
} else {
Item item = items.get(i - 1);
int benefit = item.benefit;
int weight = item.weight;
if (weight <= w) {
B[i][w] = Math.max(B[i - 1][w], B[i - 1][w - weight] + benefit);
} else {
B[i][w] = B[i - 1][w];
}
}
}
}
return B[N][W];
}
Floyd算法
实现思想
用一系列n阶矩阵来计算一个n顶点加权图的距离矩阵
矩阵D(k)的第i行第j列的元素dij (k)为从第i个顶点到第j个顶点之间最短路径的长度,并且路径的每一个中间顶点的编号不大于k
并递归地定义最优值:
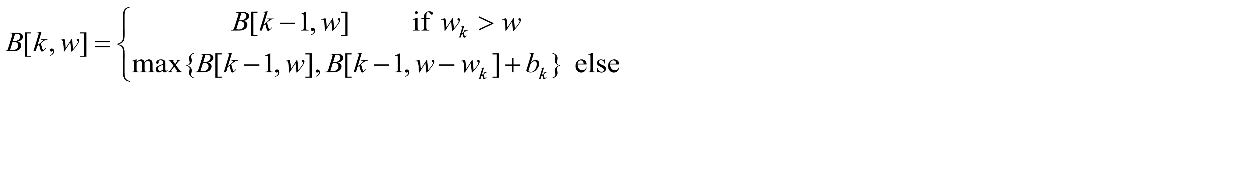
不包含第k个节点: dij (k-1)
包含第k个节点: dik (k-1) + dkj (k-1)
代码实现
// todo