数据结构回顾(一)HashMap
前言
时间越来越少,最近刷leetCode的时候发现大二学过的数据结构都有点记不得,所以现在才想狠下心来,把之前学过的东西都回顾一遍
[HashMap-> Field]
static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
Node(int hash, K key, V value, Node<K,V> next) { ... }
public final K getKey(){ ... }
public final V getValue() { ... }
public final String toString() { ... }
public final int hashCode() { ... }
public final V setValue(V newValue) { ... }
public final boolean equals(Object o) { ... }
}
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4;
static final int MAXIMUM_CAPACITY = 1 << 30;
static final float DEFAULT_LOAD_FACTOR = 0.75f;
static final int TREEIFY_THRESHOLD = 8; // 链表转红黑树阀值
static final int UNTREEIFY_THRESHOLD = 6; // 红黑树退化为链表阀值
static final int MIN_TREEIFY_CAPACITY = 64;
transient Node<K,V>[] table;
[HashMap-> put]
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}
[HashMap-> hash]
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
通过hashCode()的高16位异或低16位实现的,主要是从速度、功效、质量来考虑的,这么做可以在数组table的length比较小的时候,也能保证考虑到高低Bit都参与到Hash的计算中,同时不会有太大的开销,同时通过这种方式实现高位和低位参与hash运算,进一步避免hash冲突
[HashMap-> putVal]
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
// 1
if ((tab = table) == null || (n = tab.length) == 0)
n = (tab = resize()).length;
// 2
if ((p = tab[i = (n - 1) & hash]) == null)
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
// 3
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
e = p;
// 4
else if (p instanceof TreeNode)
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
// 5
else {
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
// 6
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}
步骤1:判断table是否为空,如果为空便创建一个
步骤2:
- 根据HashMap的长度和hash值计算出插入的元素在数组的位置,特别注意点:它通过hash& (table.length -1)来得到该对象的保存位,而HashMap底层数组的长度总是2的n次方,这是HashMap在速度上的优化。当length总是2的n次方时,h& (length-1)运算等价于对length取模,也就是h%length,但是&比%具有更高的效率。
- 由上一步计算的位置从数组中取出,如果table[i]==null,直接新建节点添加
步骤3:节点key存在,直接覆盖value
步骤4:判断是否为红黑树,如果是红黑树就在红黑树中操作,否则就在链表中操作
步骤5:
- 该链为链表
- 遍历链表,如果存在相同的key则直接覆盖value
- 否则就添加在链表最后一个节点后面
- 判断链表长度是否为8,为8就把转换为红黑树
步骤6:用于覆盖的情况,返回旧值并覆盖
步骤7:size自增并和阀值比较,判断是否需要执行扩容
[HashMap-> treeifyBin]
final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
// 1
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
// 2
else if ((e = tab[index = (n - 1) & hash]) != null) {
TreeNode<K,V> hd = null, tl = null;
do {
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
// 3
if ((tab[index] = hd) != null)
hd.treeify(tab);
}
}
步骤1:判断table数组是否为空以及是否达到红黑树的最小容量64,没有的话就进行扩容
步骤2:获取table数组hash值定位位置的链表,然后把这个单链表转换为双向链表
步骤3:把双链表转换为红黑树
[HashMap-> resize]
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
// 1
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
// 2
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
// 3
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
// 4
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
// 5
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
// ......
}
步骤1:判断旧的容量是否大于最大容量,如果是就把扩充的阀值设置为Interget.MAX_VALUE,这样就让这个HashMap不再扩容了
步骤2:判断2倍扩容后的容量是否处于最大容量和初始容量之前,如果是那就把2倍扩展之前的阀值,这里有个
细节:这里一个细节就是这个2倍扩容其实是有东西的,因为原本HashMap的容量就是2的倍数,然后现在又二倍扩容,对于后面元素迁移是有帮助,因为元素的位置要不就在原来的索引的位置,要不就在原来索引位置加上旧容量的位置
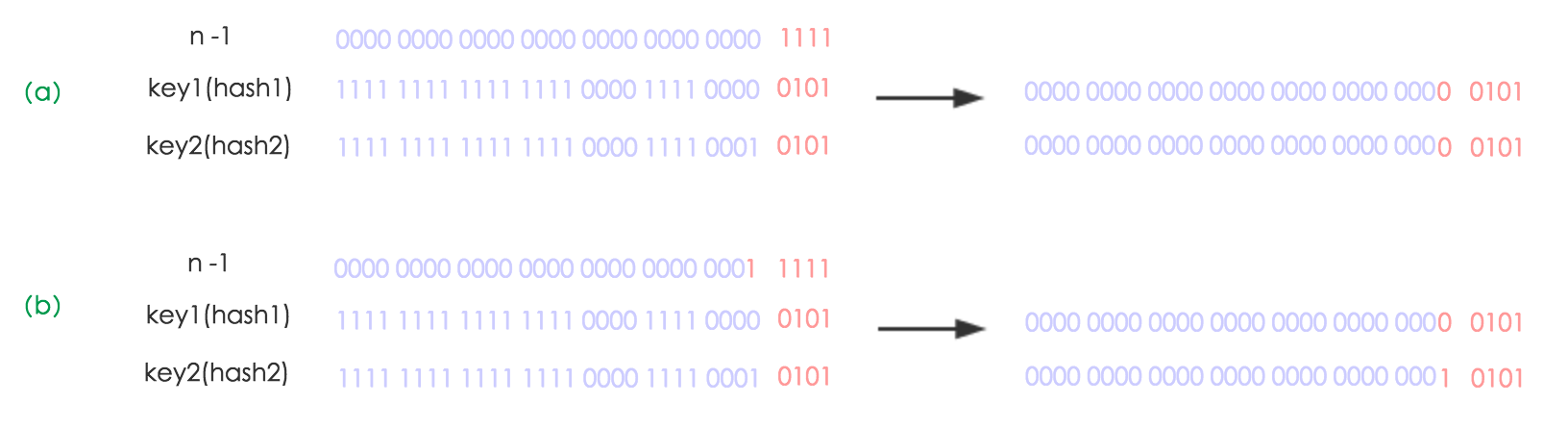
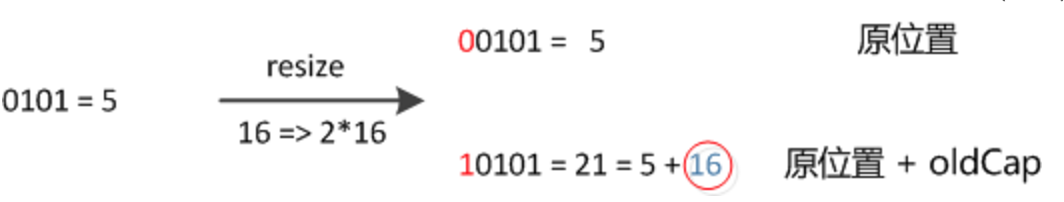
因此,我们在扩充HashMap的时候,不需要重新计算hash,只需要看看原来的hash值新增的那个bit是1还是0就好了,是0的话索引没变,是1的话索引变成原索引+oldCap,这个设计确实非常的巧妙,既省去了重新计算hash值的时间,而且同时,由于新增的1bit是0还是1可以认为是随机的,因此resize的过程,均匀的把之前的冲突的节点分散到新的bucket了
步骤3:如果之前旧的容量不大于零也就是table数组为空的这种情况下,如果此时旧的阀值大于0,新的容量就会被赋值成旧的阀值
步骤4:这种情况其实就是table数组为空,阀值也不大于0的这种情况下,容量的值就直接等于默认的init的值,然后阀值就通过load_factor乘以默认的init长度,这种情况其实才是我们平时最平常new出一个HashMap的情况
步骤5:对新的阀值进行修正,让新阀值为新容量的loadFactor倍
final Node<K,V>[] resize() {
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
// 1
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
// 2
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
// 3
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
// 4
if ((e.hash & oldCap) == 0) {
if (loTail == null) loHead = e;
else loTail.next = e;
loTail = e;
}
else {
if (hiTail == null) hiHead = e;
else hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
步骤1:对于扩容后的迁移操作区分了三种类型:单个元素,红黑树,链表,步骤1处处理的时候单个元素的情况,直接把重新hash计算该元素在新数组中的位置,然后
步骤2:判断节点是否是红黑树并执行操作
步骤3:这里的关键逻辑在注释4的if-else上,这里if-else判断的逻辑就是用来判断上面提及到的新增的位是0还是1,如果是0,则用loHead和loTail一组指针进行操作,如果是1,则用hiHead和hiTail进行操作,但是不管是用哪一组指针,操作的内容都是固定的,那就是用一个head指针指向链表的头节点,用一个tail指针指向链表的尾节点,然后分别赋值到原索引位置或者原索引+旧容量的位置
[HashMap-> get]
public V get(Object key) {
Node<K,V> e;
return (e = getNode(hash(key), key)) == null ? null : e.value;
}
[HashMap-> getNode]
final Node<K,V> getNode(int hash, Object key) {
Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
if ((tab = table) != null && (n = tab.length) > 0 &&
// 1
(first = tab[(n - 1) & hash]) != null) {
// 2
if (first.hash == hash && // always check first node
((k = first.key) == key || (key != null && key.equals(k))))
return first;
if ((e = first.next) != null) {
// 3
if (first instanceof TreeNode)
return ((TreeNode<K,V>)first).getTreeNode(hash, key);
do {
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
} while ((e = e.next) != null);
}
}
return null;
}
- 步骤1:依然是找到数组中取模位置之后链表头
- 步骤2:先判断hashCode再判断equals是否相等,不过这里有个小细节就是即便重写过equals,都会从地址开始判断,通过了就不需要走自定义的equals了,如果找的刚好是链表头的元素,就可以直接返回
- 步骤3:判断是否为红黑树,如果是则转到红黑树继续处理,如果否则遍历链表继续判断hashCode和equals找到匹配的元素
[HashMap-> remove]
public V remove(Object key) {
Node<K,V> e;
return (e = removeNode(hash(key), key, null, false, true)) == null ?
null : e.value;
}
[HashMap-> removeNode]
final Node<K,V> removeNode(int hash, Object key, Object value,
boolean matchValue, boolean movable) {
Node<K,V>[] tab; Node<K,V> p; int n, index;
if ((tab = table) != null && (n = tab.length) > 0 &&
(p = tab[index = (n - 1) & hash]) != null) {
Node<K,V> node = null, e; K k; V v;
// 1
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
node = p;
else if ((e = p.next) != null) {
// 2
if (p instanceof TreeNode)
node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
// 3
else {
do {
if (e.hash == hash &&
((k = e.key) == key ||
(key != null && key.equals(k)))) {
node = e;
break;
}
p = e;
} while ((e = e.next) != null);
}
}
if (node != null && (!matchValue || (v = node.value) == value ||
(value != null && value.equals(v)))) {
// 4
if (node instanceof TreeNode)
((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
// 5
else if (node == p)
tab[index] = node.next;
else
p.next = node.next;
++modCount;
--size;
afterNodeRemoval(node);
return node;
}
}
return null;
}
步骤1:如果要找的节点就是链表头节点,给node赋值
步骤2:如果是红黑树,则通过红黑树的方式获取待删除的节点
步骤3:如果是链表,则遍历链表然后找到待删除的节点
步骤4:如果是红黑树,则通过红黑是的方式删除节点
步骤5:删除链表节点
[Summary]
通过阅读HashMap的put和get以及扩容机制,我们解决了一些常见的问题:
- 为什么HashMap的容量是2的幂指?这是因为index=hash & (table.length-1),这个方法非常巧妙,它通过hash & (table.length -1)来得到该对象的保存位,而HashMap底层数组的长度总是2的n次方,这是HashMap在速度上的优化。当length总是2的n次方时,h& (length-1)运算等价于对length取模,也就是h%length,但是&比%具有更高的效率。
- 为什么HashMap要2倍扩容?这是因为2倍扩容可以避免rehash带来的性能开销
- HashMap是如何判断相等?先hashCode后equals
- 但是仍然有一个问题没有解决!HashMap为什么要引入红黑树?
回顾源码中涉及红黑树的部分:
- treeifyBin:
- putTreeVal:
- split:
[TreeNode-> Field]
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
TreeNode<K,V> parent; // red-black tree links
TreeNode<K,V> left;
TreeNode<K,V> right;
TreeNode<K,V> prev; // needed to unlink next upon deletion
boolean red;
TreeNode(int hash, K key, V val, Node<K,V> next) {
super(hash, key, val, next);
}
// ......
}
[TreeNode-> treeify]
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
for (TreeNode<K,V> x = this, next; x != null; x = next) {
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
// 1
if (root == null) {
x.parent = null;
x.red = false;
root = x;
}
else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
for (TreeNode<K,V> p = root;;) {
// 2
int dir, ph;
K pk = p.key;
if ((ph = p.hash) > h) dir = -1;
else if (ph < h) dir = 1;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
// 3
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp;
if (dir <= 0) xp.left = x;
else xp.right = x;
// 4
root = balanceInsertion(root, x);
break;
}
}
}
}
// 5
moveRootToFront(tab, root);
}
步骤1:遍历在[HashMap-> treeifyBin]方法中构建的双向链表,然后给根节点赋值
步骤2:取出双向链表当前位置的节点作为待添加节点,并记录key和hash,然后从红黑树的根节点开始遍历,比较添加项与当前树中访问节点的hash值判断,然后用dir保存相应的值,虽然还没看comparableClassFor和tieBreakOrder两个方法的实现,但是从步骤3就可以看到dir代表的是节点添加的路径,1表示的是右子树,-1表示的是左子树,所以整个步骤2完成的工作就是决定步骤3的插入路径,而决定的依据就是hash
步骤3:根据上一步计算出来的dir往下走,如果是叶子节点便把待插入节点插入
步骤4:红黑树的平衡操作,退出循环
步骤5:确保红黑树的根节点是tab数组对应索引的第一个
[TreeNode-> balanceInsertion]
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
x.red = true;
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
// 1
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
// 2
else if (!xp.red || (xpp = xp.parent) == null)
return root;
// 3
if (xp == (xppl = xpp.left)) {
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
// 4
if (x == xp.right) {
root = rotateLeft(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
// 5
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateRight(root, xpp);
}
}
}
}
else {
// 6
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
// 7
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
// 8
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}
步骤1:如果插入节点的父节点是否为null,这种情况x是根节点,置为黑色,无需修复
步骤2:如果插入节点父节点是黑色不需要调整,父节点红色并且爷爷节点是空也不需要调整
步骤3:这种情况就是右叔叔节点和父节点同时为红色的情况,进行修复处理
步骤4:这种情况就是右叔叔节点为空,且祖父节点、父节点和新节点不处于一条斜线上,进行左旋操作
步骤5:这种情况是右叔叔节点为空,且祖父节点、父节点和新节点处于一条斜线上,也可能是由步骤4修复得来,进行右旋操作
步骤6:这种情况就是左叔叔节点和父节点同时为红色的情况,进行修复处理
步骤7:这种情况就是左叔叔节点为空,且祖父节点、父节点和新节点不处于一条斜线上,进行右旋操作
步骤8:这种情况是左叔叔节点为空,且祖父节点、父节点和新节点处于一条斜线上,也可能是由步骤4修复得来,进行左旋操作
[TreeNode-> putTreeVal]
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {
Class<?> kc = null;
boolean searched = false;
TreeNode<K,V> root = (parent != null) ? root() : this;
for (TreeNode<K,V> p = root;;) {
// 1
int dir, ph; K pk;
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
else if ((kc == null && (kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
if (!searched) {
TreeNode<K,V> q, ch;
searched = true;
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
dir = tieBreakOrder(k, pk);
}
// 2
TreeNode<K,V> xp = p;
if ((p = (dir <= 0) ? p.left : p.right) == null) {
Node<K,V> xpn = xp.next;
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
if (dir <= 0)
xp.left = x;
else
xp.right = x;
xp.next = x;
x.parent = x.prev = xp;
if (xpn != null)
((TreeNode<K,V>)xpn).prev = x;
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}
步骤1:和[treeify]的思路大同小异,也是通过hash值去找插入方向,但是有一种比较特殊的情况就是,当初次遇到 hash 相同 key 不相同且无法利用Comparable确定搜寻方向时,会搜索左右子树来查找节点是否已存在,不存在则调用 tieBreakOrder 利用类名或hashcode来确定方向,若是接下来再次遇到这样的情况是没有必要再搜索的,直接调用 tieBreakOrder 确定方向 步骤2:根据步骤1的值判断插入到循环中查找到节点的左节点还是右节点,而且其实TreeNode还维护着一个双向链表,然后的操作就平衡以及确保红黑树的根节点是tab数组对应索引的第一个
[TreeNode-> split]
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
TreeNode<K,V> b = this;
// Relink into lo and hi lists, preserving order
TreeNode<K,V> loHead = null, loTail = null;
TreeNode<K,V> hiHead = null, hiTail = null;
int lc = 0, hc = 0;
for (TreeNode<K,V> e = b, next; e != null; e = next) {
next = (TreeNode<K,V>)e.next;
e.next = null;
// 1
if ((e.hash & bit) == 0) {
if ((e.prev = loTail) == null)
loHead = e;
else
loTail.next = e;
loTail = e;
++lc;
}
else {
if ((e.prev = hiTail) == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
++hc;
}
}
if (loHead != null) {
if (lc <= UNTREEIFY_THRESHOLD)
tab[index] = loHead.untreeify(map);
else {
tab[index] = loHead;
if (hiHead != null) // (else is already treeified)
loHead.treeify(tab);
}
}
if (hiHead != null) {
if (hc <= UNTREEIFY_THRESHOLD)
tab[index + bit] = hiHead.untreeify(map);
else {
tab[index + bit] = hiHead;
if (loHead != null)
hiHead.treeify(tab);
}
}
}
步骤1:操作和链表大同小异,不过在这里区分了高位和低位的情况后,TreeNode是以链表的方式组织起来的,而并没有直接采取红黑树的方式组织起来
步骤2:由步骤1埋下的伏笔,在赋值到tab数组的过程中,会对链表的长度做判断,如果小于6,就会从把TreeNode退化为单链表的形式,否则再构建一颗红黑树,这也是为什么要先以双向链表方式组织起来的原因了
[TreeNode-> getTreeNode]
final TreeNode<K,V> getTreeNode(int h, Object k) {
return ((parent != null) ? root() : this).find(h, k, null);
}
遍历红黑树通过hash值与key在红黑树中找到相应的节点
[TreeNode-> removeTreeNode]
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,
boolean movable) {
int n;
// 1
if (tab == null || (n = tab.length) == 0) return;
int index = (n - 1) & hash;
TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;
// 2
TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;
if (pred == null) tab[index] = first = succ;
else pred.next = succ;
if (succ != null) succ.prev = pred;
if (first == null) return;
// 3
if (root.parent != null) root = root.root();
if (root == null || root.right == null ||
(rl = root.left) == null || rl.left == null) {
tab[index] = first.untreeify(map); // too small
return;
}
TreeNode<K,V> p = this, pl = left, pr = right, replacement;
if (pl != null && pr != null) {
// 4
TreeNode<K,V> s = pr, sl;
while ((sl = s.left) != null) // find successor
s = sl;
boolean c = s.red; s.red = p.red; p.red = c; // swap colors
TreeNode<K,V> sr = s.right;
TreeNode<K,V> pp = p.parent;
if (s == pr) { // p was s's direct parent
p.parent = s;
s.right = p;
}
else {
TreeNode<K,V> sp = s.parent;
if ((p.parent = sp) != null) {
if (s == sp.left)
sp.left = p;
else
sp.right = p;
}
if ((s.right = pr) != null)
pr.parent = s;
}
p.left = null;
if ((p.right = sr) != null)
sr.parent = p;
if ((s.left = pl) != null)
pl.parent = s;
if ((s.parent = pp) == null)
root = s;
else if (p == pp.left)
pp.left = s;
else
pp.right = s;
if (sr != null)
replacement = sr;
else
replacement = p;
}
}
步驟1:通过hash找到tab数组中该位置的第一个节点,也就是我们的root节点
步骤2:判断待删除节在双向链表的视角上是否上一个节点,如果没有,就说明待删除的节点是链表头部,这个时候需要把双向链表的头结点置为待删除节点的下一节点,否则则从链表的视角上删除待删除节点
步骤3:获取根节点并且根据根节点判断红黑树的高度,如果红黑树高地太低则进行链表退化
ps:下面开始的便是红黑树的删除操作
步骤4:
- 删除操作的情况1:只有右孩子且为红色,直接用右孩子替换该节点然后变成黑色即可
- 删除操作的情况2:只有右孩子且为黑色,那么删除该节点会导致父节点的左子树路径上黑色节点减一,此时只能去借助右子树,从右子树中借一个红色节点过来即可,具体取决于右子树的情况,这里又分成两种:
- 兄弟节点是红色,则此时父节点是黑色,且兄弟节点肯定有两个孩子,且兄弟节点的左右子树路径上均有两个黑色节点,此时只需将兄弟节点与父节点颜色互换,然后将父节点左旋,左旋后,兄弟节点的左子树sl挂到了父节点p的右孩子位置,这时会导致p的右子树路径上的黑色节点比左子树多一,此时再sl置为红色即可
- 兄弟节点是黑色,那么就只能打它孩子的主意了,这里主要关注远侄子(兄弟节点的右孩子,即sr)的颜色情况,这里分成两种情况
- 远侄子sr是黑色,近侄子任意(白色代表颜色可为任意颜色),则先将s转为红色,然后右旋,再将sl换成p节点颜色,p涂成黑色,s也涂成黑色,再进行左旋即可。其实简单说就是sl上位,替换父节点位置
- 远侄子sr为红色,近侄子任意(该子树路径中有且仅有一个黑色节点),则先将兄弟节点与父节点颜色互换,将sr涂成黑色,再将父节点左旋即可
[Summary]
红黑树通过引入颜色的概念,通过颜色这个约束条件的使用来保持树的高度平衡。作为平衡二叉查找树,旋转是一个必不可少的操作。通过旋转可以降低树的高度,在红黑树里面还可以转换颜色,对比红黑树和平衡二叉树的效率得到结果:
插入:红黑树获胜:虽然说如果插入一个节点引起了树的不平衡,平衡二叉树和红黑树都是最多只需要2次旋转操作,但是平衡二叉树不平衡的概率比红黑树大,而且红黑树在不平衡的状况下还有机会通用更换节点颜色平衡,需要选择的概率相比平衡二叉树低
删除:红黑树获胜:在删除节点引起树的不平衡时,最坏情况下,平衡二叉树需要维护从被删节点到根节点这条路径上所有节点的平衡性,因此需要旋转的量级O(logN),而红黑树最多只需3次旋转,只需要O(1)的复杂度,并且和插入同理 ,平衡二叉树不平衡的概率比红黑树大,因此红黑树效率更高
查找:平衡二叉树获胜:红黑树的查询性能略微逊色于平衡二叉树因为他比平衡二叉树会稍微不平衡最多一层,也就是说红黑树的查询性能只比相同内容的平衡二叉树最多多一次比较
HashMap之所以使用红黑树这种数据结构最大的目的就是为了同时兼顾插入,删除,查找三个操作的效率
参考资料: